NerdKits - Piezoelectric Sound Meter

Piezoelectric Sound Meter

Buy a NerdKits microcontroller kit and start learning real electronics. Learn more.

NerdKits was recently a sponsor of MIT's Battle of the Bands 2009, a fundraising event which supports the Children's Miracle Network, and also is a popular gathering during MIT's Campus Preview Weekend for incoming students.

To show off our microcontroller kits during the event, we built a sound meter which uses the piezoelectric buzzer (included with our USB NerdKit microcontroller kit) in reverse, as a microphone. This provides an opportunity to demonstrate a single transistor amplifier, to make the signals from the piezoelectric element big enough for the microcontroller's analog-to-digital converter (ADC) to read.

Since our sound level meter had to be visible in a big room (the Lobdell food court in MIT's Student Center), we opted to use our bright red LED Marquee, which has 120 high-intensity red LEDs all controlled by the one ATmega168 microcontroller. We won't talk about how we built that LED array on this page -- it has its own video tutorial and related materials which you should reference for that part of the project.

Here are a few photos of the finished product: (click to enlarge)

We also have a version that runs on the 20x4 character LCD screen that's included with our kits. That way, you can build this separately from the LED array. It also provides more debugging information, such as the minimum and maximum analog-to-digital samples that were measured during each period. Click the thumbnail below to enlarge:

Analog Amplifier Details

In the video tutorial, Humberto gives an extended description of the math behind how the amplifier works. This includes concepts such as a simple model for the NPN bipolar junction transistor (BJT), biasing, how to calculate gain, and adding more gain at higher frequenies with a technique called "bypassing".

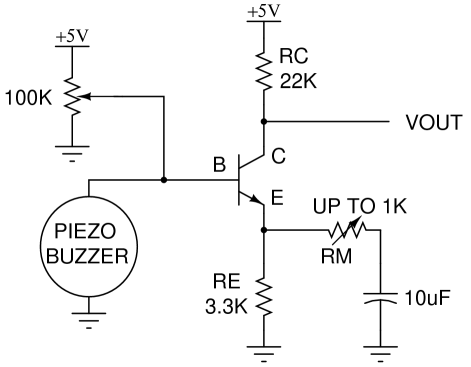
Single-transistor amplifier schematic

In the schematic above, the 100K potentiometer is adjusted until the transistor's collector current is approximately 100 microamps (10^-4 amps). This is measured with a voltmeter across R_E until the voltage is approximately 0.33 volts. Please watch the video for a full explanation of the transistor model and how we build up to this circuit.

Gain Calculation

Following along with the assumptions made in the video, and ignoring R_M and the 10uF capacitor, the gain of the amplifier is approximately 22K/3.3K = 6.7. But at higher frequencies, the 10uF capacitor looks like a short, and the gain of the amplifier is roughly 22K / (3.3K // R_M). This last part in the denominator (R_A//R_B) means the parallel combination of two resistances, which equals (R_A*R_B)/(R_A + R_B).

If the resistance loading the emitter is small, then we can't make the same assumption that we made in the video that a change in voltage at the base will necessarily be followed by an almost identical change in voltage at the emitter. Previously, the change in V_BE was small enough compared to the change in voltage across R_E. But if R_E is small or zero, the change in V_BE will become important and limit the gain of the amplifier. Here's how this comes out of the equations:

As noted in the video, the two governing equations for this simple model of the NPN bipolar junction transistor (in forward active operation) are:

I_C = β I_B
I_B = I_S e^V_BE/V_th

The first of these says that the collector current is simply β times the base current, and the second says that there is a steep (exponential) relationship between V_BE and base current. (If you're curious about numbers here, then for our 2N3904 transistor, β is typically 100-200, I_S is typically around 10^-14 amps, and V_th is about 25mV at room temperature.) Now we can also write, by definition, that the V_BE is simply the difference in voltages at the base and emitter:

V_BE = V_B - V_E

and then, for a resistance R_E between the emitter and ground, we know that V_E = R_E * I_E, and since I_E is approximately equal to I_C, V_E = R_E * I_C. We plug this in, and move V_E to the other side of the equation, to get:

V_B = R_E*I_C + V_BE

This just means that the voltage from the base to ground is a combination of the base to emitter voltage and the voltage drop across the emitter resistor R_E to ground. But this equation is interesting, because on the left side is V_B which is our input voltage, and on the right side, everything is a function of I_C, the collector current, which is related to our output voltage:

ΔV_OUT = - R_C * ΔI_C

This is just Ohm's Law for the resistor R_C -- an increase in current through it (and also through the collector) increases the voltage drop across it (which is why this is negative). We can rewrite this in a calculus way as a derivative:

dV_OUT / dI_C = - R_C

And now that the above equation connects I_C to V_OUT, to complete the full gain chain and get from V_B (the input) to V_OUT, we really just need to connect from V_B to I_C, because:

dV_OUT / dV_B = (dV_OUT / dI_C) * (dI_C / dV_B)

Fortunately, we can actually calculate (dI_C / dV_B) from the equations we wrote a few steps ago. Starting with V_B = R_E*I_C + V_BE, we can take the derivative of both sides with respect to I_C and find:

dV_B / dI_C = R_E + dV_BE/dI_C

This last little part dV_BE/dI_C can be found right out of the two transistor equations we had earlier:

I_C = β I_S e^V_BE/V_th
dI_C / dV_BE = (1/V_th) * β I_S e^V_BE/V_th

where the (1/V_th) comes from taking the derivative of the exponential. Now, we can notice that the second part of the last equation is actually I_C itself, and we can simplify:

dI_C / dV_BE = (1/V_th) * I_C
dI_C / dV_BE = I_C / V_th

or taking one divided by both sides (inverting both fractions):

dV_BE / dI_C = V_th / I_C

As we said before, V_th is about 25 millivolts at room temperature, and I_C was picked to be 100 microamps, so in this case,

dV_BE / dI_C = (0.025 volts) / (0.0001 amps)
dV_BE / dI_C = 250 ohms.

So now we can go back and substitute this in to figure out the amplifier gain:

dV_B / dI_C = R_E + dV_BE/dI_C
dV_B / dI_C = R_E + V_th / I_C
dI_C / dV_B = 1 / (R_E + V_th / I_C)
dV_OUT / dV_B = (dV_OUT / dI_C) * (dI_C / dV_B)
dV_OUT / dV_B = (-R_C) / (R_E + V_th / I_C)

So if R_E is much greater than V_th / I_C (250 ohms in this case), then we get back to our original simplified gain equation that was derived in the video, dV_OUT / dV_B = - R_C / R_E. But now if, for example, R_E = 0, then while the earlier gain equation would have suggested infinite gain (dividing by zero), our new one would suggest that it's really - 22K / (R_E + 250), or a (negative) gain of about 88 for R_M = 0. With R_M = 1K, as in our actual potentiometer in our circuit, the (negative) gain is about 18. Having a potentiometer or just swapping out resistors lets you change the gain over a wide range.

We hope we were able to present that in a useful way! Also, there's a lot of analog aspects to even a simple single-transistor amplifier like this that we didn't cover here:

input impedance of the amplifier
output impedance
transistor Early effect
saturation / clipping
other non-linear effects
modeling the piezoelectric buzzer device
frequency response
stability
and other too...

but if you're interested in further study of analog circuits, there's a lot to learn. We highly recommend the following resources:

although note that the second one expects a lot of mathematical comfort. Also, if there's interest expressed from our NerdKits customers, we can certainly start making more analog-oriented video tutorials!

Parts List

Beyond our USB NerdKit, a few extra parts are required:

Part	Quantity	Description
2N3904 NPN BJT	1	The 2N3904 is a commonly available NPN bipolar junction transistor, and certainly has the gain and frequency performanace for low-frequency applications like this one. (See manufacturer's datasheet.) Other NPN transistors, like a 2N2222, will also work fine in this application, but note that substituting a MOSFET may not produce the results you expect. MOSFETs don't have the same exponential current-voltage relationship that bipolar transistors do, so the math can be quite a bit different.
Resistors, one each of 1K, 3.3K, and 22K	3 total	Several 1K resistors (brown-black-red) are included with our USB NerdKit, but the other two sizes, 3.3K (orange-orange-red) and 22K (red-red-orange) are needed as well. Also, instead of a 1K resistor, our configuration shows a 1K potentiometer, which lets us have a continuous gain adjustment, but this is optional and not needed. With just the 1K resistor, you can still demonstrate three gain settings: R_M = infinite, R_M = 1K, and R_M = 0 (just a wire).
10uF capacitor	1	This 10uF electrolytic capacitor is needed to perform "bypassing" to get higher gain at high frequencies. Please note that this kind of capacitor is polarized, which means it can only tolerate a voltage across it in one direction. There is a lighter stripe down one side of the capacitor which is adjacent to one of the leads: this lead must connect to the lower voltage, which in this circuit is ground.

For the LED array version as shown in the video, the LEDs and overall array setup from the LED Marquee project are also needed.

A multimeter is highly recommended for building and debugging this project. We have two different models available in our store.

Source Code

The code for this project is mostly a mix of the temperature sensor code that's developed in our NerdKits Guide (using the ADC to get a value from an analog device) and the LED Marquee. There really are no new concepts on the microcontroller programming side. Here is a list of the few slight modifications we made:

One of the pins was required to for the ADC, so we had to use two less columns of the LED Array.
Since the sound meter does not need to take text from the computer, all those parts of the code have been removed, and the scrolling code was made much simpler.
font.txt was modified to make the font be "sideways." This was done because the Marquee was rotated 90 degrees so that bars would go up as noise level went up.

Since we do not expect everybody to try to make an LED Marquee, we also made a version of this code that works with just the LCD. This code measures volume the same way, and has the same amplifier described above, but instead it just prints the information to the LCD, and represents the volume bars using black characters on one row of the LCD.

For the LED array version, you can download the source code here. Start with a standard NerdKits microcontroller project and Makefile (included with the kit) and plug in this source code.

For the LCD version, you can download the source code here. Start with the standard NerdKits microcontroller project and Makefile (included with the kit) and plug in this source code.